Creating a Node-Node Connectivity Array

So for ALE/SALE, we need a connectivity array linking nodes together. Let's look again at part of our mesh:

This time, I have labelled both the cells and the nodes. Let's consider node 114 - we need to create a node-node connectivity, nodnodconn, such that:

nodnodconn[1, 114] = 113
nodnodconn[2, 114] = 118
nodnodconn[3, 114] = 56
nodnodconn[4, 114] = 57

We currently have two pieces of information which we can use to construct this connectivity:

1. The identities of the nodes surrounding any given cell (nodelist)
2. The orthogonal neighbours of any given cell (elelconn)

 Let's look at how we might map our nodnodconn array onto a simple 4 cell/9 node stencil:

Here, we would be looping over cells rather than nodes, and our aim is to create the nodnodconn entries for N0. I.e:

nodnodconn[1, N0] = N1
nodnodconn[2, N0] = N2
nodnodconn[3, N0] = N3
nodnodconn[4, N0] = N4

The positions of the node labels in the diagram shows the easiest way to access them given our orthogonal neighbour list, and remembering that nodes are numbered clockwise from bottom left, we see:

N1 = nodelist[2, C0]
N2 = nodelist[3, CR] where CR = elelconn[2, C0]
N3 = nodelist[3, CU] where CU = elelconn[3, C0]
N4 = nodelist[4, C0]

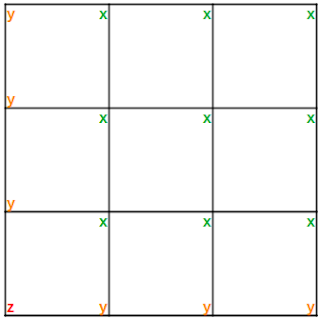
In the case where CR is zero (right-hand boundary), N2 will be set to zero. Similarly, N3 will be zero when CU is zero. This approach is not sufficient to generate a full nodnodconn array, however - consider the following mesh:

We will have full connectivity information for the nodes marked x, as these appear as the top-right node of a cell. We will not, however, currently have any information for the cells marked y and z as these will never be counted as an N0 node.

To resolve this problem, we need to do two things:

First, when setting the values of nodnodconn for each N0, we should also set the appropriate index of nodnodconn for N1 etc. according to the following rules:

nodnodconn[3, N1] = N0
nodnodconn[4, N2] = N0
nodnodconn[1, N3] = N0
nodnodconn[2, N4] = N0 

This will give us partial connectivity for the y nodes, as it will give us the links back to the x nodes. It will not, however, give us the links between y and z nodes, or indeed any information about the z node's connectivity.

To complete the array, we can use a second stencil:

So this time, for any given cell C0, we are setting nodnodconn for the bottom-left node. Again, I've marked the easiest way of getting each neighbour node:

N1 = nodelist[1, CD] where CD = elelconn[1, C0]
N2 = nodelist[2, C0]
N3 = nodelist[4, C0]
N4 = nodelist[1, CL] where CL = elelconn[4, C0]

And again, we can set the "backwards" connectivity:

nodnodconn[3, N1] = N0
nodnodconn[4, N2] = N0
nodnodconn[1, N3] = N0
nodnodconn[2, N4] = N0

By calculating nodnodconn for diagonally-opposite corner nodes, we thus ensure a fully connectivity is calculated. We can do a crude test to ensure a valid nodnodconn array by counting the number of remaining zero entries, NZ, which should obey the following rules:

• NZ = 0 for all internal nodes (node type = 0)
• NZ = 1 for all edge nodes (node type = -1 or -2)
• NZ = 2 for corner nodes (node type = -3)

The following Julia code will calculate and test the connectivity:

    # Calculate node-node conneectivity
    for c0 in 1:ncells
        n0_tr = nodelist[3, c0]
        n1 = nodelist[2, c0]
        nodnodconn[1, n0_tr] = n1
        nodnodconn[3, n1] = n0_tr

        cr = elelconn[2, c0]
        if cr > 0
            n2 = nodelist[3, cr]
            nodnodconn[2, n0_tr] = n2
            nodnodconn[4, n2] = n0_tr
        else
            nodnodconn[2, n0_tr] = 0
        end

        cu = elelconn[3, c0]
        if cu > 0
            n3 = nodelist[3, cu]
            nodnodconn[3, n0_tr] = n3
            nodnodconn[1, n3] = n0_tr
        else
            nodnodconn[3, n0_tr] = 0
        end

        n4 = nodelist[4, c0]
        nodnodconn[4, n0_tr] = n4
        nodnodconn[2, n4] = n0_tr

        n0_bl = nodelist[1, c0]

        cd = elelconn[1, c0]
        if cd > 0
            n1 = nodelist[1, cd]
            nodnodconn[1, n0_bl] = n1
            nodnodconn[3, n1] = n0_bl
        else
            nodnodconn[1, n0_bl] = 0
        end

        n2 = nodelist[2, c0]
        nodnodconn[2, n0_bl] = n2
        nodnodconn[4, n2] = n0_bl

        n3 = nodelist[4, c0]
        nodnodconn[3, n0_bl] = n3
        nodnodconn[1, n3] = n0_bl

        cl = elelconn[4, c0]
        if cl > 0
            n4 = nodelist[1, cl]
            nodnodconn[4, n0_bl] = n4
            nodnodconn[2, n4] = n0_bl
        else
            nodnodconn[4, n0_bl] = 0
        end


    end

    # Check node-node connectivity
    for node in 1:nnodes
        nzero = sum(x->x==0, nodnodconn[:, node])
        if nzero == 1
            if type[node] != -1 && type[node] != -2
                error("Invalid nodnodconn for node $node")
            end
        elseif nzero == 2
            if type[node] != -3
                error("Invalid nodnodconn for node $node")
            end
        elseif nzero >= 3
            error("Invalid nodnodconn for node $node")
        end
    end